
構造化学(教養課程)2016
担当: 岡林 潤(理学部化学科:スペクトル化学研究センター)
日時: 9/28, 10/5, 10/12, 10/19, 10/26, (11/2休講), 11/9, 11/16, (11/23), 11/30, 12/7, 12/14, 12/21, 1/11,1/16(計13回)
水曜日4限 14:55-16:40 (105分)
場所: 駒場キャンパス 1102教室
期末試験: 2017/1/24火曜日2限
構造化学特論の特別講座を行います。1/30, 1/31, 2/2
興味ある人は気軽に参加してください。他クラスの友人も誘ってくれてOKです。上級生も歓迎。
講義の目的:
何故、二原子が分子を形成するのか。量子力学を用いて理解する。
成績評価について:
期末試験がほぼ全て。レポートを6-7回出題するが、各数点程度に換算する。100点以上には加算しない。優3割ルールがある。出席はとらない。50点以下は不可となる。レポートを提出していれば、少しは救済する。
試験のみの成績分布は下記のとおり。「安心してください!」
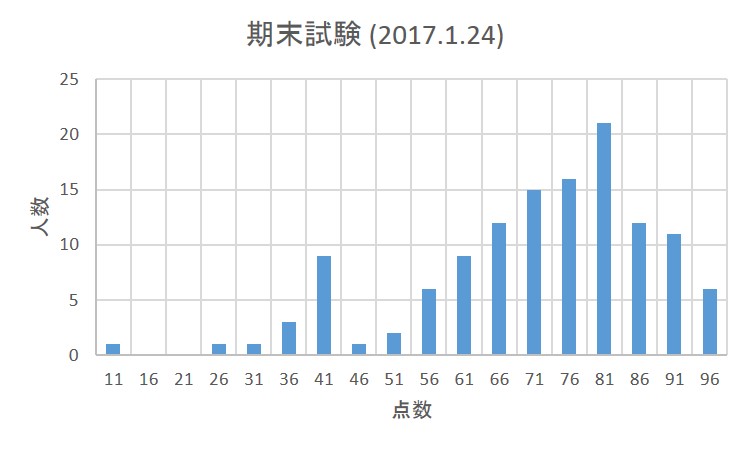
平均点 74.5点、標準偏差 15.6、講評
これにレポート点を加算し、優3割ルールによる補正をして、総合成績を算出。
点数に関する直接の問い合わせは受け付けない。教務課を通した照会にのみ応じる。
(宣伝)
理学部物理学科の先生が書いた読み物の紹介: 研究者としてうまくやっていくには
昨年度の構造化学のおまけ(構造化学特論)


2017/1/24 期末試験
期末試験、終わりました。おつかれさんでした。
おまけの問題を掲載します。物理系学科に興味ある人は考えてみてください。
課題 No.8 (1/24出題)
レポート課題 解答
第13回 2017/1/16
・総復習
第12回 2017/1/11
レポート課題 No.7 (1/11出題)
レポート課題 解答
・マイクロ波による回転スペクトル
・二原子分子の結合長の求め方について
・二原子分子の分子軌道法についての復習
第11回 2016/12/21
・マリケン、ポーリングの電気陰性度の考え方について。
・調和振動子について解説した。
・調和振動子のシュレデインガー方程式とそのエネルギーと波動関数について説明した。(証明はしていない)
・振動分光、回転分光について解説した。
【これだけはできないと...】
二原子分子の結合長の求め方を述べよ。 (期末試験より)
レポート課題 No.6 (12/21出題)
レポート課題 解答
第10回 2016/12/14
・結合次数について述べ、原子間距離との関係、何重結合かを推測できることを調べた。
・異核二原子分子の分子軌道について解説した。
・双極子モーメントが生じることを議論した。
【これだけはできないと...】
CO分子、NO分子の分子軌道を記述せよ。
第9回 2016/12/7
・σ軌道、π軌道について説明した。
・対称性によるゲラーデ、ウンゲラーデの表記について説明した。
・O2分子の電子配置を説明した。
・B2, C2, N2では、軌道間反発によりエネルギー準位に逆転が生じる。
【これだけはできないと...】
酸素分子、窒素分子の分子軌道を記述し、磁性の有無、結合次数を述べよ。
レポート課題 No.5 (12/21提出)
レポート課題 解答 (12/21掲載)
解法のヒント:
[31] 定義どうりに分子軌道の電子配置を記述し、結合次数を計算する。磁性の有無についてもコメントせよ。
[32] [31]と同様。これだけやれば、ルールが判ると思う。
[33] text(8.9)式を使い、CA, CBで偏微分して、行列式を求めよう。2. 対角化しよう。3. 近似しよう。
[34] EnとE1のエネルギー差がバンド幅になる。
[35] なかったことにしてください。できる人はchallenge !
[36] O2+の電子数に注意せよ。
[37] 水素原子の2sと2pの波動関数を教科書から持ってきて計算せよ。
[38] 有効核電荷を求める際には、[26]のルールを用いてください。
第8回 2016/11/30
・水素分子イオンH2+のエネルギーと波動関数について。
・結合性、反結合性軌道について。
・クーロン積分、共鳴積分の物理的な意味について議論した。
【これだけはできないと...】
水素分子イオンH2+のエネルギーが水素原子より低くなることを説明せよ。
第7回 2016/11/16
・有効核電荷の概念について説明した。
・イオン化エネルギーについて解説した。
【これだけはできないと...】
有効核電荷、イオン化エネルギーについて説明せよ。
レポート課題 No.4 (12/7提出)
レポート課題 解答 (12/7掲載)
解法のヒント:
[24] 定義どおりに、<x>, <x2>, <p>, <p2>を計算してみよ。
[25] 積分公式は教科書にあるものを用いよ。結果は整数となりシンプルである。物理的な意味がある。(そもそもビリアル定理とは何か、調べてみるのもよい。)
[26] 今回のハイライト。指示通りに表を作り、プロットしてみよ。有効核電荷の概念が判り、面白いはず。
[27] 上記同様に電子親和力について理解できるはず。
[28] 微分して安定点を求めよ。
[29] 誘導どおりに行ってみよう。試行関数ψは規格化されていないことに注意。つまり、1.は有限の値になる。定義どおり計算してみよ。2.は、rのみの関数なので、ラプラシアンのうちθ、φの成分はないことから、計算が楽になる。3. 相加相乗平均も使える。結果は、以前見たことのある形になり、感動するハズ!
[30] S=0とするのをヒュッケル近似といいます。変分法をしっかり復習しよう。
[..] 質問、感想、進路相談など、歓迎します。返信します。熱くがんばりましょう。
第6回 2016/11/9
・水素原子における動径分布関数、期待値について説明した。
・角運動量の量子化について説明した。
・不確定性原理について、井戸型ポテンシャルを用いて説明した。
【これだけはできないと...】
動径分布関数と期待値の違いを説明せよ。
第5回 2016/10/26
・角度方向、動径方向の方程式を導出し、解を調べた。(解いてはいない)
・1s, 2p, 3d軌道の関数形、概形を考察した。
【これだけはできないと...】
1s軌道, 2p軌道(3つ), 3d軌道(5つ)の関数形、概形を記せ。(期末試験より)
レポート課題 No.3 (11/16提出)
レポート課題 解答 (11/16掲載)
解法のヒント:
[17] 1. 電子密度は、|Ψ|2のこと
2. 動径分布関数:存在確率最大の場所
3. 期待値:平均距離
4.5 講義で説明します。感動するところ。。
[18] 講義で解説するので、スキップ
[19] テキストの球面調和関数を用いて指示通りに計算せよ。それぞれ定数になり、法則性がある。
[20] r方向の方程式(ラプラシアン)を計算(微分)する。そして、係数を比較する。答えは、Bohrモデルと一致する。
[21] r2|R(r)|2の極大値を求める。(微分する)
[22] 1. 題意より、1s軌道はrに関する0次式となる。規格化して係数を決めよ。
2. 題意より、2sの波動関数はrの1次式となり、(Ar-B)exp(-r/2a)とおける。1sとの直交性よりAとBの関係を求めよ。そして、2sの規格化により、係数を決定せよ。
[23] 誘導どおりに進めよ。
余談: 3z-r2の物理に興味のある人は、双極子モーメントに関する電磁気学の問題を解いてみよう。多重極展開と言って、ルジャンドル関数も出てきます。ここら辺は、水素原子の議論とアナロジーがあり、物理的に面白いところです。
第4回 2016/10/19
・3次元のシュレディンガー方程式を導出し、ラプラシアンを導入した。(証明はしていない)
・水素原子のシュレデインガー方程式を導出した。
・変数分離により、動径方向と角度方向に分離した。
【これだけはできないと...】
1次元井戸型ポテンシャル中の粒子の波動関数を用いて、<x>, <p>, <p2>を計算せよ。
第3回 2016/10/12
・井戸型ポテンシャルにおけるエネルギー固有値、固有関数を導出した。
・規格化について解説した。
・期待値について解説した。
【これだけはできないと...】
1次元井戸型ポテンシャル中の粒子のシュレデインガー方程式を解いて、エネルギー固有値、波動関数を求めよ。
レポート課題 No.2 (10/26提出)
レポート課題 解答 (10/26掲載)
(解法のヒント)
【12】 2. 固有値p_zとして、expで表せる。
【13】 誘導にしたがって進めよ。
【14】 8. π電子(6個)の縮退も考慮せよ。
【15】 3. 計算が面倒であるが、極座標表示では、3項から成る。(2項ではない!)
8. ℏλは物理的意味がある。Lと関係している。
【16】 題意のとおり、調和振動子のハミルトニアンに波動関数ψ を代入してみよ。xは演算子になってもxである。
第2回 2016/10/5
・波動方程式を導出した。
・ドブロイの式と波動方程式からシュレディンガー方程式を導出した。
・運動量が演算子で記述できることを示した。
・井戸型ポテンシャルにおけるエネルギー固有値、固有関数を導出した。
【これだけはできないと...】
ドブロイの関係式と波動方程式から時間に依存しない1次元シュレデインガー方程式を導出せよ。(期末試験より)
第1回 2016/9/28
・水素原子の線スペクトルを説明するには、古典力学ではできず、ボーアの量子化条件が必要であることを論じた。
・光の粒子性と波動性について論じた。
・電子の粒子性と波動性についても論じた。ドブロイ波長を導入した。
【これだけはできないと...】
水素原子について、電子の運動方程式、エネルギー保存の式、ボーアの量子条件を用いて、量子化されたエネルギーの式におけるXを求めよ。
E=X(1/n2) (期末試験より)
レポート課題 No.1 (10/12提出)
レポート課題 解答 (10/12掲載)
(解法のヒント)
【3】2.と3.の結果が一致することに驚くはずである。
【4】丁寧にプロットしてみよ。
【5】結果は知っている値になる。電卓を使って、一度自分で確かめてみよ。
【6】ボーア半径を導出できるように。
【8】イオン化の定義をしっかり理解して欲しい。
【10】発散しないためには、αが虚数になることを確かめよ。
【11】次回に繰りこし。(規格化を議論した後に。)
参考書紹介
・量子化学―基礎からのアプローチ 真船文隆 化学同人 (2008/01)
コメント: 量子化学の基礎が学べる素晴らしい本です。本講義の教科書とします。
・物理化学―分子論的アプローチ〈上〉 マッカーリ・サイモン 化学同人 (1999/12)
コメント: 量子化学をしっかり理解したい人にお勧め。判りやすい。
・実践量子化学入門―分子軌道法で化学反応が見える CD-ROM付 平山令明 ブルーバックス (2002/7)
コメント: PCを使って量子化学を楽しんでみたい人にお勧め。CD付き。構造化学の後半の理解に役立ちます。
参考ページ
2015年度 期末試験
2014年度 期末試験
2013年度 期末試験
研究紹介(理学部ニュースより)

